DQN(Deep Q-Network)系列算法解析与实践

发表于 更新于 分类于 ， 阅读次数： Waline： 本文字数： 7.4k 阅读时长 ≈ 27 分钟

1. 任务与背景介绍

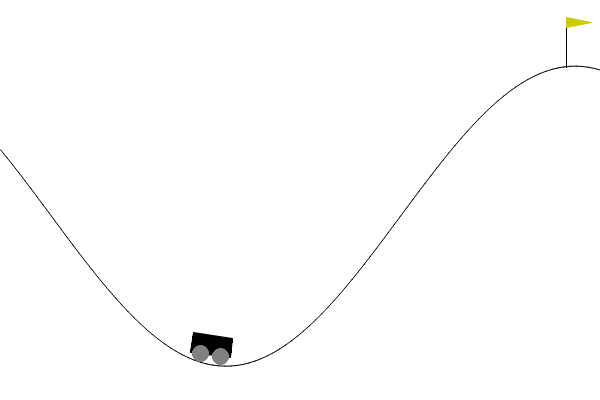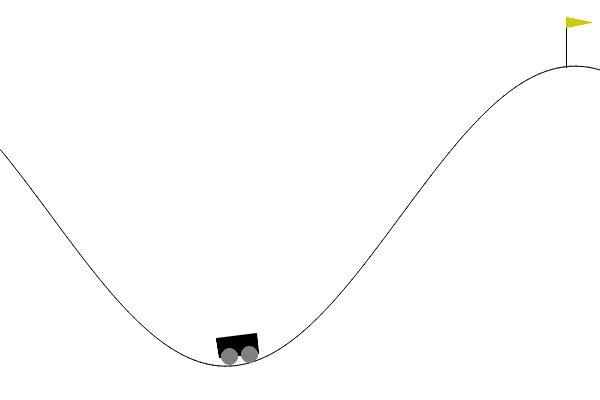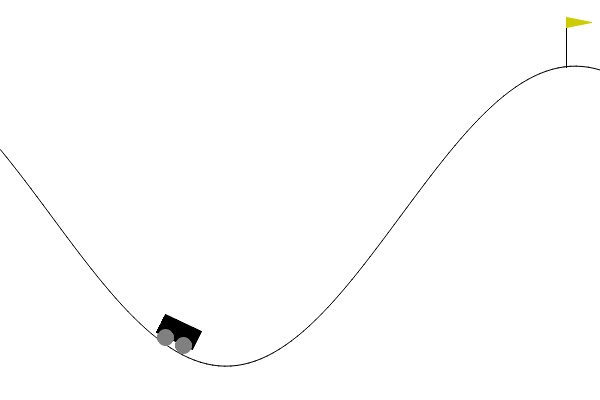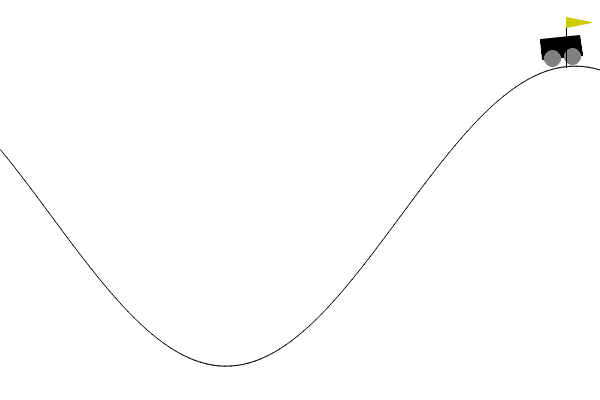
在 Gym/Gymnasium 的 MountainCar-v0 环境中，有这样一个场景：一辆小车被困在两个山坡之间，目标是到达右侧山坡顶端的红旗位置。

乍一看，这似乎只需要踩油门往右冲就行，但现实并非如此，小车的发动机动力不足，单次加速无法直接登顶，它会在半途滑落回谷底。正确的策略是先向左加速爬上左坡，然后顺势向右冲下去，再反复摆动、积累动能，最终才能冲上右侧山顶。

1.1 环境参数

在 MountainCar-v0 中，环境由以下元素构成：

  • 状态（State）：小车的水平位置与速度（连续值）
  • 动作（Action）：三个离散动作
    1. 向左加速（0）
    2. 向右加速（2）
    3. 不加速（no push）
  • 奖励（Reward）：
    • 每执行一步都会收到 -1 惩罚（鼓励尽快完成任务）
    • 到达山顶时获得额外奖励并结束回合

1.2 任务性质

这是一个离散动作空间的决策问题，适合用 DQN 解决，原因如下：

  1. 动作空间小且离散（3 个动作），可直接用 Q 值表示各动作价值
  2. 状态空间连续（位置、速度），传统 Q 表难以应用，需要神经网络来近似 Q 值函数
  3. 延迟回报明显：到达山顶的奖励需要经过一系列操作才能获得，算法必须学会权衡眼前损失与未来收益

1.3 问题难点

  • 动力不足：无法直接登顶，必须借助坡道助跑
  • 积累动能：需要多次反向加速形成足够速度
  • 奖励稀疏：过程几乎全是负奖励，只有成功登顶才有正反馈
  • 探索必要性：如果只向右加速，几乎不可能完成任务，必须探索反向助跑策略

1.4 为什么用 DQN

DQN 在此类任务中有天然优势：

  • 能学习长期回报，避免只追求即时收益
  • ε-贪婪策略让智能体有机会探索看似“错误”的操作（如向左加速），发现更优路径
  • 结合经验回放与目标网络，在连续状态空间中稳定学习高价值动作序列

2. DQN 基本原理

2.1 Q-Learning

2.1.1 Q-Learning回顾

在讲 DQN 之前，我们先回顾一下 Q-Learning，因为 DQN 其实就是 Q-Learning 在高维连续状态空间下的一种扩展。

Q-Learning 是一种 值迭代算法，核心思想是学习一个状态–动作价值函数 $Q(s,a)$，这个函数表示在状态 $s$ 下执行动作 $a$ 并按最优策略继续下去所能获得的期望回报。
它的更新公式为：
$$Q(s,a) \leftarrow Q(s,a) + \alpha \big[ r + \gamma \max{a’} Q(s’,a’) - Q(s,a) \big]$$
在离散、低维的状态空间里，Q 值可以直接用一个表（Q 表）存储，并在不断交互中更新。

如果省略学习率 α 并直接用目标替换原值，就得到核心形式：
$$Q(s, a) = r + \gamma max_{a’} Q(s’, a’) $$
这里：

  • $r$：当前动作的即时奖励
  • $\gamma$：折扣因子（0~1 之间），衡量未来奖励的重要性
  • $\max_{a’} Q(s’, a’)$表示：假设在下一个状态选择最优动作时的未来价值

2.1.2 即时奖励 vs. 未来回报

在小车登山任务中：

  • 即时奖励：每一步都是 -1（让你尽快到达山顶）
  • 未来回报：一旦到达山顶，获得额外奖励

Q-Learning 的优势在于，它会同时考虑当前奖励和未来回报。
比如，如果现在向左加速会让你离山顶更远（即时奖励差），但能积累动能从而之后登顶（未来回报高），Q 值会判断这是值得的。
这正是强化学习解决延迟回报问题的关键。

2.2 DQN

2.2.1 为什么要用深度网络替代表格？

在经典 Q-Learning 中，Q 值通常存储在一个状态-动作表（Q 表）里。但在小车登山任务中，状态是连续值（位置、速度），可能有无数个组合。如果用表格存储，每个状态都需要一行，不好存储。
于是，DQN（Deep Q-Network） 用一个神经网络来逼近 Q 值函数：

  • 输入：状态向量（位置、速度）
  • 输出：该状态下每个动作的 Q 值（3 个数）
  • 优势：不需要穷举所有状态，能在相似状态之间泛化学习成果

2.2.2 主网络 & 目标网络

DQN 有两个几乎一模一样的网络：

  1. 主网络（Online Q-Network）：每次更新时使用它来预测当前状态的 Q 值，并进行梯度下降优化。
  2. 目标网络（Target Q-Network）：在计算目标值时使用，参数更新得更慢（例如每隔 N 步从主网络复制一次）。

为什么要两个网络？
如果目标值直接由主网络实时计算，会导致更新过程不稳定，因为目标和预测值来自同一个会不断变化的网络。引入目标网络可以让目标在一段时间内保持相对稳定，从而减少训练振荡。

类比解释：“现在的自己” vs. “过去的自己”
可以把两个网络类比成：

  • 主网络 = 现在的自己（每天学习新知识，变化很快）
  • 目标网络 = 过去的自己（定期拍个快照，参考当时的想法）

学习的时候：

  • 主网络负责提出当前的理解（预测 Q 值）
  • 目标网络提供一个相对稳定的参考答案（计算目标值）
  • 过一段时间，过去的自己会更新为现在的自己（同步参数）

这种设计，让 DQN 既能快速学习，又不至于因为目标值不停抖动而陷入不稳定。

3. DQN 核心组件

3.1 主网络（Online Q-Network）

主网络（Online Q-Network） 的作用是接收当前状态 $s$（位置、速度），输出该状态下每个可能动作的 Q 值。在训练中，主网络是实时更新的，利用梯度下降不断调整参数，让预测的 Q 值更接近目标 Q 值。

在小车登山这个例子中，当小车处于“靠近左坡顶、速度向右”的状态时，主网络会输出三个数：

  • 向左加速 Q 值
  • 向右加速 Q 值
  • 不动 Q 值

算法会选择其中 Q 值最大的动作（除非在探索阶段）。

3.2 目标网络（Target Q-Network）

目标网络主要是计算目标 Q 值时使用，目的是保持一段时间内不变，减少训练振荡。更新方式其实不是每次训练都更新，而是每隔固定步数，将主网络的参数复制给目标网络。

小车登山类比：

  • 主网络 = “现在的自己”，每次都在调整思路
  • 目标网络 = “过去的自己”，一段时间才更新一次观点

这样，主网络在学习时总是参考一个相对稳定的“过去自己”，不至于因为目标值不断变化而陷入混乱。

3.3 经验回放池（Replay Buffer）

经验回放池的主要作用是存储过去的状态、动作、奖励、下一状态等（即 transition），并在训练时随机抽取一批样本进行学习。
这样做的好处有：

  1. 打乱数据相关性：环境中的数据是连续的（比如小车一直在左坡上下摆动），直接用会导致模型过拟合特定轨迹
  2. 提升样本利用率：同一条经验可以多次用于训练，而不是用一次就丢掉

还是以小车登山举例：
如果没有经验回放，小车可能连续 100 步都在左坡附近，这些相似数据会让模型短时间内“只记得左坡的事”。而有了 Replay Buffer，我们可以把过去不同位置的经验混合，让网络更全面地学习。

3.4 ε-贪婪策略

ε-贪婪策略的主要作用是在训练过程中平衡 探索（Exploration）与利用（Exploitation）。
规则：

  • 以概率 $\varepsilon$ 随机选择一个动作（探索）
  • 以概率 $1 - \varepsilon$ 选择当前 Q 值最高的动作（利用）

动态调整：通常从较大的 $\varepsilon$ 开始（更多探索），然后逐渐减小（更多利用）。

还是以小车登山例子：
刚开始，小车可能会随机向左冲、向右冲甚至不动——这有助于发现“先向左加速再向右冲顶”的策略。随着训练进行，ε 会逐渐降低，小车会更多地按照学到的最优策略去冲山顶。

这四个组件在 DQN 中缺一不可：

  1. 主网络：负责当前 Q 值预测
  2. 目标网络：提供稳定的学习目标
  3. 经验回放池：打乱相关性、提升数据利用率
  4. ε-贪婪策略：保证探索与利用的平衡

结合起来，DQN 能够在像小车登山这种连续状态 + 离散动作 + 延迟回报的任务中稳定、高效地学出策略。

4.训练流程解析

4.1 DQN网络定义

1
2
3
4
5
6
7
8
9
10
11
12
class DQN(nn.Module):  
    def __init__(self, state_dim, action_dim):  
        super(DQN, self).__init__()  
        # 两层隐层 MLP，将连续状态映射到每个离散动作的 Q 值  
        self.fc1 = nn.Linear(state_dim, 128)  
        self.fc2 = nn.Linear(128, 128)  
        self.fc3 = nn.Linear(128, action_dim)  
  
    def forward(self, x):  
        x = torch.relu(self.fc1(x))  
        x = torch.relu(self.fc2(x))  
        return self.fc3(x) # 输出形状：[batch, action_dim]，即 Q(s, ·)

4.2 模型训练实现

DQN 的大致训练流程：

  1. 初始化网络、经验池、优化器
  2. 重置环境，得到初始状态
  3. 按 ε-贪婪策略选择动作
  4. 执行动作，获取下一状态、奖励、结束标记
  5. 存储 (s, a, r, s′) 到经验池
  6. 如果经验池样本数达阈值：采样 batch，计算目标，反向传播
  7. 每隔固定步数同步目标网络参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
def train():  
    # ===== (1) 初始化网络、经验池、优化器 =====
    env = gym.make("MountainCar-v0")  
    # state: 2维 [position, velocity]
    state_dim = env.observation_space.shape[0]  
    # action: 3个离散动作：左推、无操作、右推
    action_dim = env.action_space.n  

    # 超参数
    gamma = 0.99  # 折扣因子，衡量未来奖励在当前决策中的重要程度
    epsilon = 1.0  # ε-贪婪策略初始探索率，ε1.0意味着第一回合几乎全随机选动作
    epsilon_min = 0.01  # 最小探索率，保留一小部分随机动作（1% 概率），防止策略僵化
    epsilon_decay = 0.995  # 每回合结束后对 ε 做指数衰减（更快收敛）
    lr = 1e-3  # 学习率，控制每次参数更新的步幅大小
    batch_size = 64  # 批量大小，每次从经验池里采多少条样本来更新网络
    target_update_freq = 500  # 目标网络更新频率，每隔多少环境步同步一次目标网络
    max_episodes = 600  # 最大训练回合数
    memory_size = 50000  # 经验回放池容量
  
    # 构建主网络 & 目标网络（结构相同）  
    online_net = DQN(state_dim, action_dim)  
    target_net = DQN(state_dim, action_dim)  
    target_net.load_state_dict(online_net.state_dict())  # 初始先对齐
    optimizer = optim.Adam(online_net.parameters(), lr=lr)  

    # 经验回放池：存储 (s, a, r, s′, done)
    memory = deque(maxlen=memory_size)  
  
    total_steps = 0  
    for episode in range(max_episodes):  
        # ===== (2) 重置环境，得到初始状态 =====
        state, _ = env.reset()  
        total_reward = 0  

        # 一个回合最多 200 步（MountainCar的默认上限）
        for t in range(200):  
            total_steps += 1  
  
            # ===== (3) 按ε-贪婪策略选择动作 =====
            # 以ε的概率做随机动作（探索），否则选Q值最大的动作
            if random.random() < epsilon:  
                # 探索：从动作空间随机采一个动作，0（左加速）、1（不动）、2（右加速）
                action = env.action_space.sample()  
            else:  
                # 利用
                with torch.no_grad():  
                    # [position, velocity] -> tensor
                    state_tensor = torch.FloatTensor(state).unsqueeze(0) 
                    # 把当前状态输入DQN主网络，得到每个可能动作的Q值 -> [1, action_dim]
                    q_values = online_net(state_tensor)  
                    # 找出Q值最大的动作的索引(最优动作)
                    action = q_values.argmax().item()  
  
            # ===== (4) 执行动作，获取下一状态、奖励、结束标记 =====
            next_state, reward, terminated, truncated, _ = env.step(action)  
            done = terminated or truncated  
  
            # ---- 奖励塑形（可选）----
            # 这里额外加了 abs(position - (-0.5))，鼓励远离谷底（-0.5）向两侧移动，
            # 使学到“先左后右”的策略更容易出现（尤其在稀疏奖励场景）。 
            position, velocity = next_state  
            reward += abs(position - (-0.5))  
  
            # ===== (5) 存储 (s, a, r, s′, done) 到经验池 =====
            memory.append((state, action, reward, next_state, done))  

            # 状态推进到下一步
            state = next_state  
            total_reward += reward  
  
            # ===== (6) 如果经验池样本数达阈值：开始学习 =====
            # 这里用“> 1000”作为启动学习的阈值，避免一开始样本过少导致过拟合/发散
            if len(memory) > 1000:  
                batch = random.sample(memory, batch_size)  
                states, actions, rewards, next_states, dones = zip(*batch)  

                # 转张量
                states = torch.FloatTensor(states) # [B, state_dim]
                actions = torch.LongTensor(actions).unsqueeze(1) # [B, 1]
                rewards = torch.FloatTensor(rewards).unsqueeze(1) # [B, 1]
                next_states = torch.FloatTensor(next_states) # [B, state_dim]
                dones = torch.FloatTensor(dones).unsqueeze(1) # [B, 1] (1.0/0.0)
  
                # (6-2) 主网络预测当前 Q 值：Q(s,a)
                # online_net(states) -> [B, A]，gather挑出实际执行的动作a的Q值
                q_values = online_net(states).gather(1, actions)  # [B, 1]
  
                # (6-3) 目标网络计算下一个状态 s′ 的最大Q值：max_a' Q_target(s′, a′)
                with torch.no_grad():  
                    next_q_values = target_net(next_states).max(1)[0].unsqueeze(1)  # [B, 1]
                    # 对终止状态不进行 bootstrap：*(1 - done)
                    # (6-4) 构造目标：y = r + γ * max Q_target(s′, a′)
                    target_q = rewards + gamma * next_q_values * (1 - dones)  
  
                # (6-5) 计算损失并反向传播（这里用 MSELoss）
                loss = nn.MSELoss()(q_values, target_q)  
                optimizer.zero_grad()  
                loss.backward()  
                optimizer.step()  
  
            # ===== (7) 每隔固定步数同步一次目标网络参数 =====
            if total_steps % target_update_freq == 0:  
                # 将主网络的最新参数拷贝给目标网络，稳定目标值的估计
                target_net.load_state_dict(online_net.state_dict())  
  
            if done:  
                break  

        # ε 衰减：每回合结束后降低探索比例，最终不低于 epsilon_min
        epsilon = max(epsilon_min, epsilon * epsilon_decay)  
  
        # 训练日志：Steps 是本回合步数；Reward 是“原始奖励 + 塑形奖励”的总和
        print(  
            f"Episode {episode + 1}/{max_episodes} | Steps: {t + 1} | Reward: {total_reward:.2f} | Epsilon: {epsilon:.3f}")  
  
    # 训练完成，保存主网络（即推理时使用的在线网络）参数
    torch.save(online_net.state_dict(), "dqn_mountaincar_fast.pth")  
    print("模型已保存到 dqn_mountaincar_fast.pth")

4.3 日志输出

1
2
3
4
5
6
7
8
9
10
11
12
13
Episode 1/600 | Steps: 200 | Reward: -191.07 | Epsilon: 0.995
Episode 2/600 | Steps: 200 | Reward: -181.50 | Epsilon: 0.990
Episode 3/600 | Steps: 200 | Reward: -192.44 | Epsilon: 0.985
...
Episode 178/600 | Steps: 200 | Reward: -146.89 | Epsilon: 0.410
Episode 179/600 | Steps: 163 | Reward: -112.88 | Epsilon: 0.408
Episode 180/600 | Steps: 200 | Reward: -127.69 | Epsilon: 0.406
...
Episode 597/600 | Steps: 97 | Reward: -57.98 | Epsilon: 0.050
Episode 598/600 | Steps: 134 | Reward: -93.57 | Epsilon: 0.050
Episode 599/600 | Steps: 88 | Reward: -56.04 | Epsilon: 0.050
Episode 600/600 | Steps: 112 | Reward: -74.69 | Epsilon: 0.049
模型已保存到 dqn_mountaincar_fast.pth

日志说明：

  • Episode X/Y：第 X 回合，总共 Y 回合训练
  • Steps: S：本回合用的步数（最多 200 步，MountainCar-v0 是默认 200 步终止）
  • Reward: R：本回合的总奖励（这里是原始奖励 + 奖励塑形后的结果），MountainCar 原始奖励：每步 -1，到达终点额外奖励 0，所以当没有奖励塑形时，每步都会让总奖励更负。因为代码中加了奖励塑形，所以奖励值不是纯整数，而是会出现 -191.07、-57.98 这种小数。
  • Epsilon: E：当前 ε-贪婪策略的探索率，随着回合增加而衰减，代表模型更倾向于利用而不是探索。

4.4 验证模型效果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def evaluate():
    # === 1. 加载训练好的 DQN 模型 ===
    # MountainCar 状态 2 维(位置、速度)，动作 3 种(左加速、右加速、不加速)
    model = DQN(state_dim=2, action_dim=3)  
    model.load_state_dict(torch.load("dqn_mountaincar_fast.pth"))
    model.eval()  # 切换到评估模式（关闭 Dropout / BN 等训练特性）

    # === 2. 创建环境（渲染模式） ===
    env = gym.make("MountainCar-v0", render_mode="human")

    num_episodes = 10      # 测试回合数
    success_count = 0      # 成功登顶的次数计数

    # === 3. 循环执行多个评估回合 ===
    for episode in range(num_episodes):
        state, _ = env.reset()  # 重置环境，获取初始状态
        done = False            # 回合是否结束
        step = 0                # 当前回合步数计数

        # === 4. 单个回合循环 ===
        while not done:
            env.render()        # 渲染画面（显示小车运动）
            time.sleep(0.02)    # 控制动画播放速度（不然会很快看不清）

            # 将状态转换为张量，并加 batch 维度 [1, state_dim]
            state_tensor = torch.FloatTensor(state).unsqueeze(0)

            # 用训练好的模型计算 Q 值，并选择 Q 值最大的动作
            with torch.no_grad():  # 评估时不计算梯度（节省内存和加速）
                q_values = model(state_tensor)
            action = q_values.argmax().item()  # 取最大 Q 值对应的动作编号

            # 在环境中执行这个动作
            state, reward, terminated, truncated, _ = env.step(action)
            done = terminated or truncated  # 终止或超时都算回合结束
            step += 1

        # === 5. 回合结束后，判断是否成功到达右侧山顶 ===
        if state[0] >= 0.5:  # MountainCar 目标位置是 0.5
            success_count += 1

        # 打印该回合的执行结果
        print(f"Episode {episode + 1} | Steps: {step} | Final Pos: {state[0]:.2f}")

    # === 6. 计算总的成功率 ===
    success_rate = success_count / num_episodes * 100
    print(f"成功率: {success_rate:.2f}%")

    env.close()  # 关闭环境窗口
1
2
3
4
5
6
7
8
9
10
11
Episode 1 | Steps: 173 | Final Pos: 0.54
Episode 2 | Steps: 152 | Final Pos: 0.54
Episode 3 | Steps: 154 | Final Pos: 0.54
Episode 4 | Steps: 87 | Final Pos: 0.51
Episode 5 | Steps: 86 | Final Pos: 0.52
Episode 6 | Steps: 86 | Final Pos: 0.51
Episode 7 | Steps: 161 | Final Pos: 0.54
Episode 8 | Steps: 179 | Final Pos: 0.54
Episode 9 | Steps: 167 | Final Pos: 0.54
Episode 10 | Steps: 156 | Final Pos: 0.54
成功率: 100.00%

日志说明：
1. 成功率100% 表示模型已经学会稳定地冲上右侧山顶（终点位置 ≥ 0.5），每回合都完成任务，训练效果非常好，没有偶发失败的情况。

2. 步数差异

  • 步数范围 86 ~ 179 步 → 虽然都能成功，但到达速度不完全一致
  • 较短的回合（86~87 步）说明模型走的是比较高效的冲顶路线
  • 较长的回合（170+ 步）可能是因为初期动作探索了更多，不是最短路径，但仍能完成任务

3. 最终位置

  • Final Pos 0.51~0.54 → 每次登顶都刚好过终点线，MountainCar 到达 0.5 就算成功，所以模型倾向于“够用就好”，到达目标就停止
  • 没有出现明显的“冲太远”或“差一点没到”的情况，策略很稳定

模型已经完全学会 MountainCar 任务的关键策略（先反向加速积累动能，再加速冲顶），并且稳定性极高，几乎没有失败风险。不同回合的步数差异主要来自动作选择的细微差异，而非策略不稳定。

5.目标函数与公式解析

5.1 目标：让预测 Q 值更接近“正确答案”

在 DQN 中，神经网络的任务是去拟合 $Q(s,a)$，也就是，当前状态 s 下执行动作 a，未来能获得多少回报。而我们希望 预测的 Q 值 和 目标 Q 值 越接近越好。
因此，用均方误差（MSE） 来衡量两者差距：
$$L(\theta) = \big( Q(s,a;\theta) - y \big)^2$$
其中：

  • $Q(s,a; \theta)$：当前 主网络（Online Q-Network）的预测值，即对未来回报的估计
    • $s$：当前状态（比如小车的位置和速度）
    • $a$：当前动作（向左、向右、不动）
    • $\theta$：神经网络的参数（权重和偏置等）
  • $y$：目标值（Target Q）

5.2 目标 Q 值的计算

目标值 y 来源于 贝尔曼方程（Bellman Equation）：
$$y = r + \gamma \cdot max_{a’} Q_{\text{target}}(s’, a’)$$
含义：

  1. $r$ ：当前动作获得的即时奖励
  2. $\gamma$ ：折扣因子（0~1），控制未来奖励的重要性
  3. $\max_{a’} Q_{\text{target}}(s’, a’)$：在下一个状态 s’ 中，选择最优动作 a’ 能获得的最大价值（由目标网络计算）
    换句话说：目标 Q = 即时奖励 + 未来可能的最大奖励（折扣后）

5.3 为什么要用目标网络（Target Q-Network）

如果目标值也用当前网络计算，就会出现，当前网络的参数在更新，目标值也跟着变，这会导致训练过程不稳定（Q 值像踩着自己影子）。

解决办法是引入一个 延迟更新 的目标网络 $Q_{\text{target}}$，每隔 N 步，把主网络参数在复制到目标网络中。

5.4 为什么要 detach() 目标值

在 PyTorch 里，如果不加 .detach()，$y$ 会被认为是计算图的一部分，误差回传时，梯度会一路回传到目标网络，这样目标网络也会被更新（这不是我们想要的）。

而我们希望只更新主网络参数 $\theta$，目标网络只是一个固定参考，不会被梯度影响。

所以在代码中是这样：

1
2
3
with torch.no_grad():  # 或 .detach()
    next_q_values = target_net(next_states).max(1)[0].unsqueeze(1)
    target_q = rewards + gamma * next_q_values * (1 - dones)

这样，target_q 不会产生梯度。

5.5 整个过程类比

可以把主网络和目标网络想象成：

  • 主网络（现在的自己）：正在学习，更新很频繁
  • 目标网络（过去的自己）：阶段性保存下来的“笔记”，在一段时间内不变，作为稳定的参考
  • 训练目标：现在的自己尽量学得跟过去的“稳定版本”一致，但未来会更新过去的版本

6.Double DQN（解决 Q 值过高估计）

6.1 问题点

DQN 目标值计算存在高估风险

1
2
3
4
5
6
with torch.no_grad():
	# target_net(next_states) 是用 目标网络 预测所有可能动作的Q值
	# .max(1)[0] 直接选最大值，这个操作既选择动作又用这个最大值作为评估值
	# 如果预测里有噪声（预测值有偏差），max会偏向取偏高的那个，从而产生乐观偏差
    next_q_values = target_net(next_states).max(1)[0].unsqueeze(1)
    target_q = rewards + gamma * next_q_values * (1 - dones)

假设目标网络预测：

1
2
3
动作 0: 5.0  (真实应是 4.8)
动作 1: 4.6  (真实应是 4.6)
动作 2: 4.9  (真实应是 4.9)

因为预测的噪声，动作 0 被预测得高了一点（5.0），max 会选它，并直接把 5.0 当作真实价值。
一次两次还好，但每轮更新都会不断把最大值往高的方向推这就会导致Q 值虚高。

6.2 策略

为了避免这个问题，Double DQN 分两步：

1
2
3
4
5
# 1. 用主网络选择下一个状态的最优动作
next_actions = online_net(next_states).argmax(1).unsqueeze(1)
# 2. 用目标网络评估这个动作的 Q 值
next_q_values = target_net(next_states).gather(1, next_actions)
target_q = rewards + gamma * next_q_values * (1 - dones)

这样动作选择（argmax）用的是主网络，而动作评估（gather）用的是目标网络。两个网络参数不同，噪声就不会同步放大，从而可以降低过高估计，提高稳定性，在MountainCar-v0 case中， Double DQN可以让 Q 值估计更平稳，不会盲目认为某个方向的冲刺能立刻成功，从而减少无效尝试。

6.3 完整实现

https://github.com/keychankc/dl_code_for_blog/blob/main/027_DQN_code/mountainCar_double_DQN.py

6.4 成功率对比

DQN vs Double DQN 实现的成功率对比：

1
2
3
===== 成功率对比（100 回合） =====
DQN         | 成功率: 99.00%  | 平均步数: 125.60 | 平均终点位置: 0.52
Double DQN  | 成功率: 100.00% | 平均步数: 115.60 | 平均终点位置: 0.51

7.Dueling DQN（分离状态价值与动作优势）

DQN是直接用一个神经网络输入状态 $s$，输出每个动作 $a$ 对应的 Q 值，所有 Q 值都是一层网络直接回归出来的，没有显式区分状态价值和动作优势。

Dueling DQN则是改了最后几层的结构，把 Q 值拆分成：

  1. 状态价值 $V(s)$ ：当前状态本身的好坏，不依赖于具体动作
  2. 动作优势 $A(s,a)$ ：在当前状态下，不同动作之间的相对优劣

最后再合成：$Q(s,a) = V(s) + A(s,a) - \frac{1}{|\mathcal{A}|} \sum_{a’} A(s,a’)$，减去平均优势是为了去中心化，避免 $V(s)$ 和 $A(s,a)$ 的数值相互冲突。
所以：

  • DQN “一个脑子同时管状态和动作的价值”
  • Dueling DQN “一个脑子负责状态价值，另一个脑子负责动作差异”

7.1 为什么要这样拆分

在很多状态下，动作选择不敏感。
举个 MountainCar 例子：

  • 当小车已经在山顶或者刚出发速度很慢时，左右加速的效果差别不大，这时动作优势 $A(s,a)$ 接近 0，主要由 $V(s)$ 决定状态价值
  • DQN 在这些状态下还是会为每个动作都单独学 Q 值，效率低
  • Dueling DQN 可以直接先学 $V(s)$，不用反复去学相似的 Q 值，从而收敛更快

7.2 Dueling DQN 的优势

  1. 泛化性更好：类似状态下的价值能被快速共享，减少重复学习
  2. 学习更稳定：在动作选择不重要的状态里，仍能准确评估状态价值
  3. 适用于在稀疏奖励任务：因为它能先学会哪些状态接近目标，再去细化动作优势

MountainCar-v0 中的任务目标是先积累动能再冲顶。在上坡的中段，左右加速的效果差别很大 → 依赖 $A(s,a)$ 来学优势。在坡底加速积能时，左右加速的差别没那么大 → 依赖 $V(s)$ 来学状态价值。
结果就是，DQN 可能在不重要的状态浪费学习资源，而Dueling DQN 能更快聚焦在真正关键的动作选择时刻（比如冲顶前一两秒）。Dueling 架构能更快学到“山谷是低价值区域，山顶是高价值区域”。

7.3 完整实现

https://github.com/keychankc/dl_code_for_blog/blob/main/027_DQN_code/mountainCar_dueling_DQN.py

7.4 成功率对比

DQN vs Double DQN vs Dueling DQN 实现的成功率对比：

1
2
3
4
===== 成功率对比（100 回合） =====
DQN          | 成功率: 99.00% | 平均步数: 123.66 | 平均终点位置: 0.51
Double DQN   | 成功率: 100.00% | 平均步数: 122.57 | 平均终点位置: 0.51
Dueling DQN  | 成功率: 100.00% | 平均步数: 126.50 | 平均终点位置: 0.53

8. Prioritized Experience Replay（优先经验回放）

8.1 PER 和 DQN 的关系

DQN的核心思想是用经验回放（Replay Buffer） 打破样本之间的时间相关性，提升样本利用率。但 DQN 默认 均匀随机采样（Uniform Sampling）——每个样本被选中的概率一样，不管它对学习有多重要。
PER（Prioritized Experience Replay） 是 DQN 的一个改进策略，它只改“采样”这一步，把经验池里的样本按照学习价值高低来调整被采样的概率。

  • 学习价值高 → 采样概率高（重点训练难学的、错误大的样本）
  • 学习价值低 → 采样概率低（减少浪费在早就学会的简单样本上）

所以，PER 是 DQN 的一个升级版本，DQN 的其他部分（Q 网络、目标网络、损失函数等）都可以保持不变，只要改“怎么从经验池抽样”。

8.2 PER 的原理

在 DQN 中，每个训练样本的 TD 误差（Temporal-Difference Error）是：
$$\delta_i = y_i - Q(s_i, a_i)$$

  • $Q(s_i, a_i)$：当前网络预测的 Q 值
  • $y_i = r_i + \gamma \max_{a’} Q_{\text{target}}(s’_i, a’)$：目标 Q 值
  • $|\delta_i|$ 表示当前预测和真实目标的差距。

PER 认为：

  • 差距大（|δ| 大） → 当前模型预测不准，这个样本对学习的帮助大 → 采样概率应该高
  • 差距小（|δ| 小） → 模型已经学得差不多，这个样本对学习帮助有限 → 采样概率可以低一些

采样概率公式：
$P(i) = \frac{|\delta_i|^\alpha}{\sum_k |\delta_k|^\alpha}$

  • α 控制优先程度（α=0 就退化为均匀采样）
  • TD 误差大 → 概率高

另外，为了防止高概率样本被重复学习过多，PER 会配合重要性采样权重（IS weight） 做修正，保证训练无偏性。

8.3 PER 在 MountainCar-v0 中的意义

MountainCar 是一个稀疏奖励 + 延迟奖励任务，普通 DQN 学得慢的原因之一是：

  • 大部分时间，小车动作对最终奖励影响很小（例如卡在坡中间的微调动作）
  • 真正关键的状态（比如冲顶前的几个动作、助跑的反向加速）出现概率很低，如果采样不够多，网络很难学到

PER 的作用：

  • 放大关键瞬间的学习频率：当网络第一次成功冲顶时，这些状态的 TD 误差会很大，PER 会让它们在后续训练中反复出现，强化记忆
  • 减少浪费时间在无关状态：对已经学会的坡底慢速动作，TD 误差会变小，采样概率降低

这样，MountainCar 用 PER 收敛速度会比普通 DQN 快很多，尤其是在早期探索到关键路径时。

8.4 完整实现

https://github.com/keychankc/dl_code_for_blog/blob/main/027_DQN_code/mountainCar_PER_DQN.py

8.5 成功率对比

1
2
3
4
5
===== 成功率对比（100 回合） =====
DQN         | 成功率: 100.00% | 平均步数: 122.94 | 平均终点位置: 0.52
Double DQN  | 成功率: 100.00% | 平均步数: 120.32 | 平均终点位置: 0.51
Dueling DQN  | 成功率: 100.00% | 平均步数: 121.35 | 平均终点位置: 0.53
PER DQN      | 成功率: 100.00% | 平均步数: 119.92 | 平均终点位置: 0.52

MountainCar-v0 这个任务太简单了，状态空间低维（2维），而且目标非常明确，DQN 本身就足够解决得很好， Double DQN、Dueling DQN、PER DQN 三个改进点在这里的性能提升几乎看不出来。

9.总结与延伸

​方法​ ​核心改进​ ​任务优势​ ​适用场景​
​原始DQN​ 神经网络拟合Q值函数 基础解决方案，适合简单任务 低维状态空间，动作选择明确的任务
​Double DQN​ 解耦动作选择与价值评估 减少Q值高估，策略更稳定 需长期策略的任务（如延迟回报明显）
​Dueling DQN​ 分离状态价值(V)和动作优势(A) 更快识别关键状态，减少冗余学习 动作影响差异大的任务（如冲刺关键期）
​优先经验回放(PER)​​ 按TD误差优先级采样 加速收敛，聚焦关键经验 稀疏奖励或关键样本稀少的任务
补充说明​：
  1. 在MountainCar-v0中，因任务简单（状态仅2维），所有方法均能100%成功，改进版优势不明显
  2. 若环境更复杂（如高维状态/稀疏奖励），改进方法（尤其是Dueling+PER组合）的收敛速度和稳定性优势会更显著

10. 备注

环境：

  • mac: 15.2
  • python: 3.12.4
  • pytorch: 2.5.1
  • numpy: 1.26.4
  • gymnasium: 1.2.0
  • box2d-py: 2.3.8

完整代码：
https://github.com/keychankc/dl_code_for_blog/tree/main/027_DQN_code